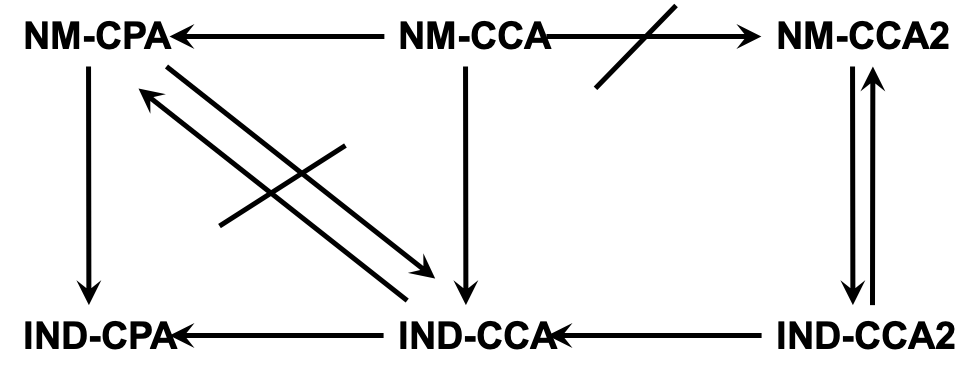
1. Indistinguishable Chosen Ciphertext Attack¶
Exists a decryption oracle such that, the adversary tricks Alice to decrypt a “ciphertext”. For Alice, she will only decrypt message \(c\) if \(c\) looks “random” enough.
The adversary’s job is to create a ciphertext which looks like a legitimate ciphertext (not simply replay attack).
Example:
Let \(C = (c_1, c_2, \cdots, c_l)\) be the encryption of plaintext \(B = (b_1, b_2, \cdots, b_l)\). Malice wants to learn \(B\) from \(C\) with CCA.
Malleability
In CCA, Malleability is an important property. If an encryption algorithm is malleable, Malice can generate another ciphertext by manipulating one ciphertext.
1.1. Multiply-by-y-attack¶
Malice computes \(C' = (yc_1, yc_2, \cdots, yc_l)~mod~n\). Alice willl decrypt \(C'\) to create \(B' = (b_1', b_2', \cdots, b_l')\). Because according to Euler’s Theorem, exists \(ab~mod~N \in QR_N\) iff 1) \(a \in QR_n\) and \(b \in QR_n\) 2) \(a \in QPseudoR_n\) and \(b \in QPseudoR_n\). (We have to write \(QPseudoR_n\) because \(QNR_p\) requires \(p\) to be prime.)
If \(y\) is bit \(1\), multiply \(y\) on bit \(b_i\) it flipping \(b_i\). Malice can recover \(B\) by flipping certain bits in \(B'\) according to \(y\).
We must make sure \(C'\) looks random. So choose \(Y=(y_1, y_2, \cdots, y_l)\) rather than \(Y = (y, y, \cdots, y)\).
1.2. Attack Using CCA¶
Abuse RSA
Malice picks a random number \(r \in \mathbb{Z}_n^*\) and compute \(c' = r^e c\). Because \(r\) is randomly chosen, so \(c'\) looks random and Alice should decrypt it.
Alice decrypts the ciphertext \(D(c') = D(r^e m^e) = rm~mod~n\) and returns the result to Malice.
Malice gets message by \(m = rm \cdot m^{-1}~mod~n\).
Abuse Rabin’s Algorithm
Theorem
Let \(n=pq\) and \(y \in QR_n\). The 4 square roots of \(y\) has the following properties
they are all distinct from one another
\(x_1 + x_4 = x_2 + x_3 = n\)
\(gcd(x_1+x_2, n) = gcd(x_3+x_4, n) = q\) and \(gcd(x_1+x_3, n) = gcd(x_2+x_4, n) = p\)
For example. Rabin’s algorithm uses public key \((N, b) = (209, 183)\), and the four decryption roots for the ciphertext 31 are 185, 204, 31, 60. These four roots will be returned to Malice. Malice computes \(gcd(31+185, n) = gcd(204+60, n) = q\), then \(p = n \cdot q^{-1}\)
The solution to CCA is “Plaintext Aware Encryption”. The ciphertext involves more structures which do verification job.
1.3. Plaintext Aware Encryption¶
A PKC system is plaintext aware if it is computationally infeasible for an adversary to produce a “valid” ciphertext rather than noise without the knowledge of the plaintext.
Another explanation from Coding Theory is that all valid ciphertexts are viewed as points in a high dimensional space. Points are placed so random that there is no patten for the adversary to find a transformation function from one point to another.
This is Random Oracle Model (ROM) for Security, i.e. ROM combines plaintext aware and semantic security to obtain non-malleable encryption scheme. This means the attacker cannot modify content of a message i.e. \(E(M_1) = C_1\) and \(\nexists C' s.t. C'=E(M_1')\) where \(M_1, M_1'\) are both valid and related plaintext.
Also, security against to Adaptive CCA is equivalent to Non-Malleability.
1.4. Random Oracle Model¶
Random Oracle has a deterministic algorithm that gives true uniform distribution as output.
ROM is used for giving security proof \(\Rightarrow\) provable security model.
ROM goes beyond ad-hoc models for protecting against IND-CCA.
ROM has two parts:
Oracle
A deterministic algorithm with true randomness \(G\)
Simulator (Simon simulator)
simulates anybody’s oracle.
A random oracle can be emulated/simulated in PPT.